Severe analytical problems in dendroclimatology, part twelve

This post attempts to explain just why the attempted signal enhancement technique known as RCS detrending fails to properly retrieve the climatic trend from tree rings. There’s a brief review of some points made previously and then some conceptually new material.

In previous posts in this series I’ve shown repeatedly that the RCS method of removing the tree age/size effect (“detrending”), so as to enhance the environmental signal, will not return an accurate estimate whenever there is an environmental (typically, climatic) trend present in the data. In the last post in this series I tried to explain that the RCS method can be thought of as a “natural experiment”, wherein one tries to estimate and remove that age/size effect, via the creation of a “Regional Curve” (RC) constructed from trees growing at different times, which thereby presumably sample the full range of different climate states experienced over that time. The RC is nothing more than a smoothed average of the ring response (usually, ring width) for each age/size in the sample (age being the traditional metric). This ~ mean response is then removed from each individual tree core, the presumption being that what remains then represents the non-biological trend, i.e., the environmental signal. [Note as an aside, that I use the term “environmental” rather than “climatic” for a reason; even if one has successfully removed the biological noise trend from the data, this by itself does not guarantee that one has necessarily extracted a climatic signal, and in turn, a putatively extracted climate signal does not guarantee that one has obtained the specific climatic parameter of interest. Obtaining the latter from tree rings is not an easy task; there is a virtual gauntlet of potential problems that has to be worked through].

What I have not gone into great detail on so far is the rationale as to why this problem arises. In fact, that rationale underlies the very reason that I began to address this whole topic in the first place; I didn’t just accidentally stumble upon the fact that RCS produces bad results and wonder why. Theoretical considerations, when combined with known dendroclimatology practices, predict apriori, the kind of problems I’ve been discussing to date; that’s very important. And this issue is a very major problem when you consider that there are no better methods that can be applied to tree ring data: RCS was itself the proposed solution to the even more problematic methods that arise when trying to detrend each core individually (the “segment length curse” of Cook et al (1995)), which is simply mathematically impossible. Better methods just do not exist (I have developed one, but haven’t even discussed it yet here, or submitted for publication because I’ve had such tremendous difficulty in getting people to understand that there’s any problem that needs fixing in the first place).

So, once again as review: (1) the RCS method will not recover existing climatic trends whenever biological trends also exist, under common field sampling practices, (2) it will not recover such trends even when no such complicating biological trend exists, and (3) it will very frequently distort actual long-term variance (i.e. trend) into short term (inter-annual) variance, thereby causing inaccuracies at both time scales. These problems are all independent of all other tree ring analysis issues that have been addressed to date, and they are also basal, in that the first step in any tree ring analysis must be to remove the non-environmental trend from the data. If you don’t get that right, all subsequent analyses with the data will carry the error right on through. That’s why this is such an important problem.

OK, onward. The following graph describes the essential reason for the problem. It represents information from a Dahurian Larch (Larix gmelinii or Larix dahurica depending on authority) site from the Alagea river region of Siberia, covering the period from 1608 to 1991. The lines in the graph all show either (1) sample sizes for a given calendar year (right axis, red and green step-type lines), or (2) the mean ring age for the sample (left axis, black and blue lines). Focus for now on the two black lines.

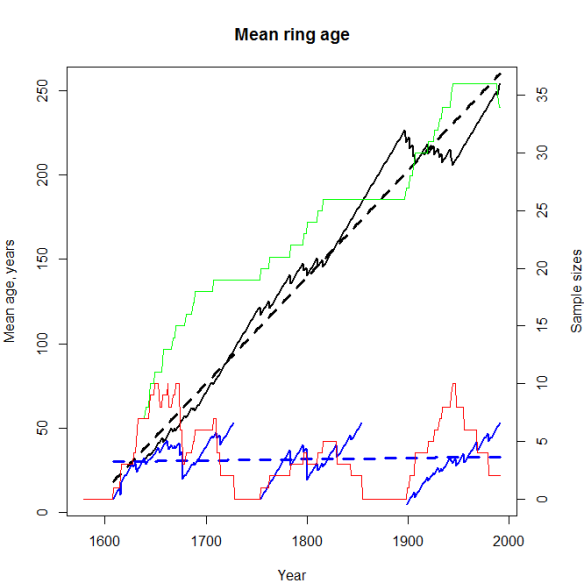
The solid black is the mean ring age (or “cambial” age; the ring number from tree center) per year, and the dashed black is a linear regression line fit to that. We can see that the mean ring age of the sample rises steeply and almost continuously over time. The reason for this is that each sampled tree extends from whatever year of its first measured ring, all the way to the end of the chronology (1991), which the green line shows as a +/- continually increasing sample size over time. The origins of the different tree cores (n = 36) are evident wherever the slope of the solid black line turns briefly negative: the rings of a new young tree decrease the mean ring age slightly for a year, but then the mean age immediately starts to increase again steadily, continuing until the next young tree enters the sample. This site is better than most (much better), in that tree start dates are fairly well scattered across the chronology length (1607-1991); I’ll get to the importance of that toward the end.

So here’s the problem. The sample size is increasing over time, which means that the oldest rings in the sample occur only in the later years of the chronology. If there is an environmental trend over time, then when the Regional Curve is constructed (to estimate and remove the age/size effect), that part of the curve representing the oldest, largest trees, will be biased towards whatever environmental state occurred in the later years of the chronology, and that part of the curve representing the youngest, smallest trees will be biased toward the state occurring when they were formed. Stated differently, the RCS age/size effect estimate will inadvertently contain environmental trend information in it. In a site like this one, where the tree starts are temporally well dispersed, the bias in the younger rings will be minimized pretty well (though not perfectly). But the older rings will be a problem: because each tree continues growing right up to 1991, the bias imparted to the later rings on each tree induce a progressively increasing bias to the mean of the detrended rings for each calendar year, thereby keeping them from tracking the true environmental signal. The effect is always to bias the estimated environmental trend towards zero, i.e. to under-estimate its magnitude.

Now look at the blue lines. The solid blue (discontinuous) line shows the mean ring age obtained if I truncate each ring series to the length of the shortest series in the sample, which is 53 years in this case. This is a drastic data castration, a big loss of data, and I do it only in order to remove the bias just described. It produces a data set in which rings of different age are all well scattered throughout the chronology, and therefore should do a much better job of estimating the age/size effect without confounding by environmental trend signals. [To be absolutely clear, this is not in any way cherry picking to achieve a pre-selected result, but rather an attempt to reduce a bias whose origin, and hence potential remedy, are known]. A linear regression line (dashed blue) fit to these data show zero trend in mean ring age, as expected.

This is a really useful application of the idea of a natural experiment, i.e. choosing data so as to specifically reduce the confounding effect between two independent variables that otherwise make all results unreliable. There is however a big drawback: it greatly reduces the sample size in each year, as shown clearly by the red line. Some years in fact have no sample at all, others contain only one or two cores, and even the very best years are sampled by no more than ten cores, which will translate to somewhere between five and ten trees, since one or two cores are taken from each tree. Nevertheless, we might get some important information out of this tradeoff, at least whenever the annual sample sizes are toward the higher end of the range. So I’ll run an RCS computation over both the original, non-truncated data, and this truncated data, using ring area as the response variable. Here’s what I get:

The black line represents the non-truncated data (i.e. traditional RCS analysis); blue line the truncated data and sample sizes by the green and red again. To be sure, the sample sizes are small and the results therefore uncertain, but there are two time periods in which the core sample size ranges +/- continuously between five and ten (~= 3-7 trees): 1635-1710 and 1910-1975. In both cases, the estimate returned by the truncated data differs noticeably from that of the full data set, either in its absolute value, the short term trend over the specified interval, or both. [The large difference around the 1840s occurs when the sample size drops to only two or three cores and is not emphasized here]. This information is of course limited–the sample sizes do not allow for a full length reconstruction with the truncated data–but nevertheless, it provides some empirical evidence that the bias induced by the process described above might in fact be substantial in real data, and that a very different environmental signal might thus be returned when better accounted for.

I can explore this issue much more fully with simulated data, not hampered by these sample size issues, and am doing so. As long as the sample size is high enough, it’s absolutely clear that artificially reducing the series lengths like this fully solves this problem. The problem is that very few existing field samples at the ITRDB archive have the needed sample size to allow this drastic data truncation. There are a few however, and I’m in the process of evaluating them. Some of them contain sub-fossil wood samples (centuries-old wood preserved by cold and either extreme dryness or extreme wetness). In bogs especially these data are much less susceptible to this problem, since the trees do not get particularly old and therefore there is no chance of including really old rings in the sample and creating the described problem.

However, there is another very major issue here when it comes to using this method as a potential remedy for the application of RCS to existing tree ring data sets (besides the low sample size issue). This goes back to the point I made above about this Alagea site having particularly well spaced tree start dates. This reality alone allowed me to truncate each series so as to get all tree ages/sizes +/- well mixed over the full time period. But this situation is in fact pretty rare: most sites at the ITRDB data archive do not achieve a good dispersion of tree start dates throughout. This statement is based on an analysis of the set of ~ 500 Schweingruber/Birmensdorf sites which I am in the process of analyzing, but there is no particular reason to expect the other 3000+ sites archived at the ITRDB would be significantly different. I computed a diagnostic metric that ranges over [0,1], with 1.0 representing perfectly staggered start dates and 0.0 representing perfectly even-aged stands. The vast majority of values in this data set are < 0.5 and many are < 0.25, meaning that the sites tend strongly toward the even aged end of the spectrum.

When stands reach a certain even aged threshold, data truncation becomes an impossible solution, because so much data is removed that no significant sample size remains to extend into the typical instrumental data/calibration period of say, 1880-1980, and certainly not enough to allow a good sample size over both calibration and validation periods. Sometimes there is no overlap at all. Recall that in the first graph the slope of the dashed blue line was near zero. This is what we need, as that represents no overall bias potentially induced by the tree age/size issue explained above. But what we will get for most sites instead is exemplified by this graph, from another larch site of about the same total length, from a different region of Siberia (the Kuonomka River area):

Here the slope of the mean age for the truncated data (dashed blue) is not only not near zero, there is also no data at all after about 1800.

Conclusion

The upshot of all of this is that, tree ring size is an extremely problematic predictor of past climatic trends. This is due to the fact that
(1) ring size has a very pronounced tree age/size effect (even after removing the purely geometric effect on ring width by converting to ring area), an effect that must be removed to accurately retrieve the desired environmental signal (typically climatic),
(2) the best available method for doing this, RCS, has serious problems in accomplishing this goal, that arise from a combination of the existence of the age/size effect and the unbalanced age/size structure present in many/most existing data sets, and
(3) a potential fix for such imbalance described here, involving an approximation of a natural experiment in which individual ring series are truncated, is likely to be useful on only a small fraction of existing tree ring size data sets, those with a large number of sampled cores having tree start dates well spaced throughout time.
(4) the tree ring width data from a very large fraction of the existing tree ring archive are thus very likely not useable for the purpose of estimating anything other than variation on short time scales. A completely different field sampling focus is needed for future data collections, one which focuses on collecting many cores from trees of all possible different ages/sizes, with subsequent analyses focused on young to middle aged trees, avoiding older trees.
(5) I haven’t yet talked about wood density–that’s another matter entirely. I will get into those issues in a future post; density holds much more promise than does ring size, for archived data.